SISTEMAS DIGITALES:TABLAS DE VERDAD
Operadores lógicos
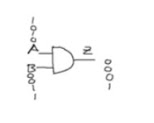
Y AND
Función de AND
1:Se necesita una entrada A, un entrada B y una salida Z ,luego las ubicamos en la tabla de verdad.
2:Como tenemos dos variables independientes que son A y B ,se necesita de 4 renglones en orden canónico .
3:El and solo va a ser verdadero cuando ambos valores de entrada sean verdaderos.
4:Si A esta en 0 y B en 0 ,Z va a ser 0
5:Si A esta en 0 y B en 1 ,Z va a ser 0
6.Si A esta en 1 y B en 0 ,Z va a ser 0
7:Si A esta en 1 y B en 1 ,Z va a ser 1
Por lo que la tabla queda de la siguiente forma:
Representación del AND
El and se representa como una multiplicación con los signos * ∙ ^
Z=m*n
Z=m ∙ n
Z=m ^ n
En AND solo va a ser 1 cuando todas las entradas sean simultáneamente un 1.
0 0 = 0
0 1 = 0
1 0 = 0
1 1 = 1
O OR
Función de OR
1:Se necesita una entrada A, una entrada B y una salida Z, luego ubicarlas en la tabla de verdad.
2:Si A esta en 0 y B en 0 ,Z va a ser 0
3:Si A esta en 0 y B en 1 ,Z va a ser 1
4:Si A esta en 1 y B en 0 ,Z va a ser 1
5.Si A esta en 1 y B en 1 ,Z va a ser 1
Representación del OR
El OR se puede representar por el símbolo +
Z= A+B
Esto quiere decir que en OR solo basta que 1 de las variables de entrada sea verdadera para que la salida sea también verdadera.
0 0 = 0
0 1 = 1
1 0 = 1
1 1 = 1
BUFFER
Función de BUFFER
1: Se necesita una entrada A y una salida Z
2: Si A esta en 0 ,Z va a ser 0
3: Si A esta en 1 ,Z va a ser 1
Representación de BUFFER
Se representa mediante un triangulo ,colocando en la parte izquierda la entrada A y en la parte de la punta la salida Z.
En BUFFER lo mismo que se tiene de entrada se tiene de salida.
0 = 0
1 = 1
NOT
Función de NOT
1: Se necesita una entrada A y una salida Z
2: Si A esta en 0 ,Z va a ser 1
3: Si A esta en 1 ,Z va a ser 0
Denotar negación
/A
Para denotar la negación es por medio de un circulo ,donde en la parte izquierda se colocara la entrada A y en la parte derecha se colocara la /A negada .
En NOT si la entrada es 0, se va a convertir en un 1, y si es 1, se va a convertir en 0.
0 = 1
1 = 0
EJEMPLO
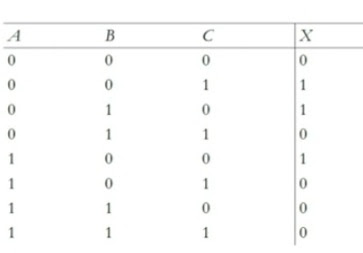
Expresión X(A,B,C) = /AB+C+BA/C
Se calcula la expresión la cual va a ser el resultado de X
Para conocer los valores de esta función, se necesita realizar la tabla de verdad donde se coloca las entradas A ,B Y C ,además de la salida X ,
2^2=4
2^3=8
Para rellenar esta tabla se deben seguir los siguientes pasos:
1:Se debe colocar la lista de variables independientes A, B, Y, C ,además de una variable dependiente X.
2:En la variable C ,se colocan un patrón de un 0, 1, 0 ,1 ,0 y así hasta ocupar la cantidad de renglones que se necesite.
3:En la variable B se colocan de dos en dos ;como 0, 0, 1, 1 ,0, 0, 1, 1 y así sucesivamente
4:En la variable A se colocan cuatro 0 y cuatro 1
Cuando tenemos una tabla de verdad con todas las posibles combinaciones de las variables independientes ,se va a tener un tipo de tabla llamada TABLA CANONICA.
Esta va a esperar que los reglones estén ordenados numéricamente en binario.
Las variables independientes deben ir a la izquierda y la variable dependiente o el resultado a la derecha.
Resultado
Z X(A,B,C)=(0,1,1,0,1,0,0,0)
0












Comentarios
Publicar un comentario